钢纤维混凝土弯曲疲劳性能研究
仰建岗,刘伟,王秉纲
0 前言
在混凝土中掺入钢纤维能显著地提高混凝土的抗拉强度、抗弯拉强度、抗冻性、抗冲性、抗磨性和抗疲劳性能。在路面工程中应用可以明显减薄面层厚度,提高路面使用功能和耐久性。本文在实验研究的基础上,综合钢纤维的体积率和长径比对SFRC弯曲疲劳特性的影响,提出了新的弯曲疲劳方程,供修订混凝土路面设计规范时参考。
1 普通混凝土弯曲疲劳方程
对疲劳方程的问题,国内外许多学者和机构进行大量的研究工作,主要采取单对数和双对数两种不同形式的疲劳工程。Feret首先进行了混凝土的弯曲疲劳试验,其后Kesler、Galloway、Hus Wirschilling、Mcall、Ballinger、永松静也等人都对混凝土材料的弯曲疲劳特性进行了分析研究,他们采用单对数形式在加载次数N为102~107范围内得出线性疲劳方程序结构
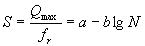
式中,Qmax--反复应力最大值;
fr--混凝土的弯拉强度;
a,b--疲劳试验确定的系数。
Darter在弯拉疲劳试验结果基础上,整理出失效概率为50%时的回归系数a=1.0,b=0.0568。比利时的Veverka等得出的试验结果为a=1.0,b=0.05。
式(1)所地的疲劳方程,是在低应力保持不变(等于或接近于0)而施加不同级位高应力的循环加荷情况下得到的。但实际上混凝土面层随的是行车荷载和温度两方面的交替作用。没有行车荷载时,面层受到幅度变化的温度应力的反复作用,构成了混凝土所承受的循环应力的低应力。当作用有行车荷载时,面层承受荷载和温度的综合反复作用,此综合应力构成了循环应力的高应力。因而,混凝土面层受到的是高、低应力反复作用。为了使疲劳方程反映出这种加荷情况对混凝土疲劳寿命的影响,挪威的Aas-jaconson在式(1)中引入一项低应力与高应力之比的系数R,下述形式的疲劳方程
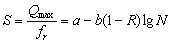 (2) (2)
式中, 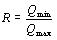
这种形式的疲劳方程较好地反映了混凝土的疲劳寿命随低应力的提高而增加并呈线性关系的规律。Aas-Jascbson通过试验得到的系数值为a=1.0,b=0.064。随后Tepfers以主西班牙的Farriga等都采用不同的低应力进行了混凝土试件受拉(劈裂)和受压的疲劳试验,也证实了上述关系式。Farriga得出的试验系数为a=1.0,b=0.091。Tepfers得出在S≥0.80时试验结果的离散性很大。
同济大学也采用不同低应力进行了混凝土的弯曲疲劳试验,得到在失效概率50%时式(2)形式的疲劳方程,系数为a=0.999,b=0.0724,同时整理得到相关性很好的双对数形式的疲劳方程
lgS=lga-0.0422(1-)lgN (3)
式中,a--回归系数。
西安公路交通大学(现长安大学)针对目前交通组成中超、重载较多从而引起混凝土板实际应力水平较高的情况,重点作了应力水平在0.85以上的室内小梁弯曲疲劳试验,同样得到相关性很好的双对数形式疲劳方程(保证率50%)
lgS=lga-0.0388(1-)lgN (4)
我国现行水泥混凝土路面设计中,对普通混凝土路面的疲劳应力系数的规定,主要考虑荷载应力和温度应力对路面的作用,通过室内小梁试验得到考虑应力重复作用的疲劳方程
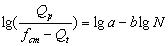 (5) (5)
式中, 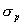 --荷载疲劳应力,MPa; --荷载疲劳应力,MPa;
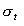 --温度疲劳应力,MPa; --温度疲劳应力,MPa;
fcm--混凝土弯拉强度,MPa;
α、b--回归系数
由式(5)可得
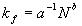 (6) (6)
由于水泥混凝土路面面板的受力状况与室内小梁试验不尽一致,并考虑一定的保证率,在规范中选取系数b=0.0516和a=1.0。从而得到疲劳应力系数关系式
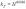 (7) (7)
式中,  为考虑设计使用年限内荷载应力累计疲劳作用的疲劳应力系数。 为考虑设计使用年限内荷载应力累计疲劳作用的疲劳应力系数。
2 SFRC疲劳方程
SFRC优良的耐疲劳特性,主要来自于SFRC的阻裂能力。而阻裂能力的高低又直接受纤维间距和界面效应的影响。通过对SFRC实验数据回归分析可以得出考虑钢纤维的体积率和长径比的疲劳方程。与普通混凝土弯曲疲劳方程相仿,SFRC的弯曲疲劳方程也有单对数和双对数形式,如公式(8)和公式(9)。整理由切削型钢纤维配制的SPRC的弯曲试验数据(114组),单对数疲劳方程的一般形式为公式(10),双对数疲劳方程形式如公式(11)
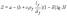 (8) (8)
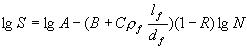 (9) (9)
以上两式中, 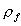 的为钢纤维的体积率, 的为钢纤维的体积率,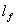 为钢纤维的和度, 为钢纤维的和度,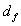 为钢纤维的等效直径, 为钢纤维的等效直径, 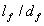 即为钢纤维的长度直径比,简称长径比。 即为钢纤维的长度直径比,简称长径比。
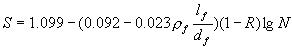 (10) (10)
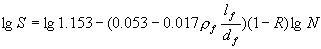 (11) (11)
为了得到99.87安全保证率,减去3倍回归误差 ,由式(10)得单对数疲劳方程 ,由式(10)得单对数疲劳方程
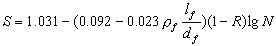 (12) (12)
同样为了得到99.87%安全保证率,减去3倍回归误差 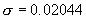 ,由式 (11)得双对数疲劳方程 ,由式 (11)得双对数疲劳方程
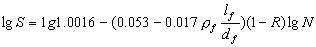 (13) 对于熔抽型钢纤维,文献[3,4]提出,当熔抽纤维体积率为1.0%时,经室内小梁疲劳试验得出的疲劳方程为 (13) 对于熔抽型钢纤维,文献[3,4]提出,当熔抽纤维体积率为1.0%时,经室内小梁疲劳试验得出的疲劳方程为
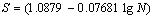 +(0.03597+0.02039lgN)R/2 (14) +(0.03597+0.02039lgN)R/2 (14)
当特重、重交通量时R取0.1,中等和轻交通量时R取0。R取0.1时,公式(14)可变成为
S=1.09927-0.07817(1-R)lgN (15)
将熔抽型钢纤维试验数据(12组)代入式(15),回归成公式(8)的单对数疲劳方程,与式(10)相同,同样减去3倍回归误差可得式(12)。类似地,可得到双对数形式的疲劳方程
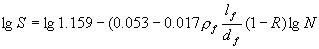 (16) (16)
与式(11)基本相同,减去3倍回归误差可近似得式(13)
对文献[8]提出的熔抽型纤维的疲劳方程
单对数:R=0.15, S=1.1012-0.0699lgN
R=0.20, S=1.1048-0.066lgN
双对数:lgS=lg1.1280-0.04016(1-R)lgN
与本文建立的疲劳方程
单对数: R=0.15, S=1.099-0.0686lgN
R=0.20, S=1.099-0.0629lgN
双对数:lgS=lg1.153-0.04314(1-R)lgN
进行了比较后可知两种方程基本相同。
现行混凝土路面设计规范,荷载的疲劳影响以疲劳系数的形式表示在荷载疲劳应力计算公式[2]中。由双对数疲劳方程得疲劳系数公式(7)。因此,由式(13)取a=1.0可得SFRC疲劳系数
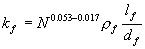 (17) (17)
在疲劳方程的建立过程中,分别采用了直线和二次曲线拟合,并对线性疲劳方程与二次曲线疲劳方程进行对比.通过对比分析得知,二次曲线方程的相关系数值略高于线性方程。对疲劳方程的建立影响不大。为了与现行规范保持一致,仍采用线性疲劳方程。
3 比较与分析
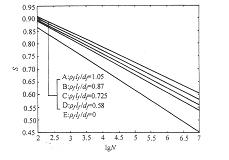
SFRC疲劳方程与素混凝土疲劳方程的最大不同点是包含了钢纤维体积率 、钢纤维长径比 、钢纤维长径比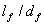 ,即在混凝土基材中掺入不同体积率和长径比的钢纤维。因此,SFRC的疲劳性能不仅受混凝土基材疲劳特性的影响,而且, ,即在混凝土基材中掺入不同体积率和长径比的钢纤维。因此,SFRC的疲劳性能不仅受混凝土基材疲劳特性的影响,而且,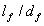 是影响疲劳寿命的重要因素。我国有关设计规范中,没有SFRC疲劳应力系数的规定,只是简单套用较早的普通混凝土路面的疲劳方程,加上钢纤维的体积率和长径比对疲劳性能的影响。本文在SFRC的疲劳试验数据的基础上,进行回归得出了切削型SFRC的疲劳方程。同时对熔抽型SFRC进行了分析。得出熔抽型SFRC与切削型SFRC的疲劳方程基本一致。图1为不同 是影响疲劳寿命的重要因素。我国有关设计规范中,没有SFRC疲劳应力系数的规定,只是简单套用较早的普通混凝土路面的疲劳方程,加上钢纤维的体积率和长径比对疲劳性能的影响。本文在SFRC的疲劳试验数据的基础上,进行回归得出了切削型SFRC的疲劳方程。同时对熔抽型SFRC进行了分析。得出熔抽型SFRC与切削型SFRC的疲劳方程基本一致。图1为不同 的钢纤维混凝土与普通混凝土的疲劳特性的比较。从图中可以看出:当疲劳寿命N相同,应力比S随 的钢纤维混凝土与普通混凝土的疲劳特性的比较。从图中可以看出:当疲劳寿命N相同,应力比S随  增大而提高,当N为106时,应力比S分别为0.606,0.624,0.642, 0.664。而普通混凝土的应力比S为0.482。可见,SFRC的疲劳强度得到显著的提高。当应力比S一定时,SFRC疲劳次数N明显增大。 由 增大而提高,当N为106时,应力比S分别为0.606,0.624,0.642, 0.664。而普通混凝土的应力比S为0.482。可见,SFRC的疲劳强度得到显著的提高。当应力比S一定时,SFRC疲劳次数N明显增大。 由 0.58增大到1.05时,疲劳次数分别为5.426×105,9.732×105,1.843×106,4.414×106。与普通混凝土的疲劳次数为1.389×104相比,疲劳次数可提高2个数量级,抗疲劳性能得到极大的提高。 0.58增大到1.05时,疲劳次数分别为5.426×105,9.732×105,1.843×106,4.414×106。与普通混凝土的疲劳次数为1.389×104相比,疲劳次数可提高2个数量级,抗疲劳性能得到极大的提高。
图1
4.结语
本文充分考虑钢纤维的影响,求得了SFRC的应力比S,疲劳寿命N, 者之间的关系。在实验的以及R四基础上,经过回归分析,建立SFRC的疲劳方程,单对数形式为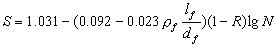
双对数形式为 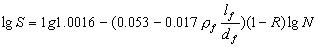
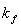 并提出了疲劳系数 的表达式为 并提出了疲劳系数 的表达式为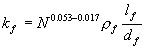
与规范方法相比,所提出的疲劳方程和疲劳系数更加合理,可供修订规范时参考使用。
(摘自《公路交通科技》2002年第2期) |


